UNDERSTANDING ASTRONOMICAL REFRACTION

Gambar seperti di atas biasa digunakan untuk menjelaskan pembelokan cahaya dalam medan gravitasi matahari sesuai prediksi Einstein dalam Teori Relativitas Umum yang diumumkan pada tahun 1916.

Cara pembuktian yang diusulkan Einstein dilaksanakan oleh tim ilmuwan negara Inggris,  dipimpin oleh Sir Arthur Eddington.  Berdasarkan data dari Royal Astronomical Society, Arthur Eddington membidik kelompok bintang Hyade dari kota Oxford di Inggris waktu malam hari pada bulan Januari dan Februari 1919.  Setelah itu bersama timnya Eddington berangkat menuju pulau Principe di sebelah Barat Afrika, dan membidik Hyade pada saat gerhana matahari tanggal 29 Mei 1919 di kota Roca Sundy.   

Pada bulan Mei 1919 itu cuaca di atas Principe kurang menguntungkan karena berawan, demikian juga menjelang saat gerhana. Namun Eddington berhasil memotret gerhana yang berlangsung sekitar 6 menit 30 detik. Dan penyimpangan cahaya hasil perhitungan Arthur Eddington adalah 1,62 detik busur,  mendekati hasil perhitungan Einstein 1,75 detik busur.

Cara pembuktian hipotesis sesuai yang diusulkan oleh Einstein selaku pencetus teori,  seharusnya tidak bisa dilaksanakan,  mengingat bahwa dalam keilmiahan ilmu astronomi berlaku pengamatan dalam waktu seketika.  Maksudnya, semua perhitungan untuk menentukan posisi sejati ( True Position ) dan Posisi Semu ( Apparent Position ) suatu bintang di langit hanya berlaku pada saat dan pada tempat pengamatan itu dilakukan.

Pengamatan sebuah bintang yang sama dan dilakukan dua kali dari tempat yang berbeda posisi geografinya, akan menghasilkan tinggi dan asumut bintang yang berbeda.  Tinggi dan asumut bintang menunjukkan posisi bintang  pada saat pengamatan itu dilakukan.  Tinggi dan asumut bintang  berubah setiap saat disebabkan karena gerakan sehari-hari dari benda angkasa.  tersebut.  Oleh sebab itu, cara pembuktian seperti yang dilakukan oleh Arthur Eddington, seharusnya tidak bisa dilakukan.  Lebih-lebih lagi pengamatan / pemotretan bintang yang dilakukan dua kali itu berbeda waktunya cukup lama.    Hasil pembuktian yang dilakukan oleh Arthur Eddington pada tahun 1919  itu harus ditolak, karena tidak ilmiah. 

Dalam Astronomi, pembelokan cahaya adalah suatu hal yang biasa,  dan bukan disebabkan oleh medan gravitasi benda massif,  melainkan karena terjadinya refraksi cahaya ( refraction of light ).  Refraksi cahaya menyebabkan cahaya dari semua benda-benda angkasa yang sampai ke bumi dan dilihat oleh pengamat, telah dibelokkan oleh media yang dilaluinya,  termasuk dibelokkan oleh atmosfer bumi. Besarnya penyimpangan cahaya dalam astronomi dikenal dengan sebutan ‘ lengkungan sinar astronomis ‘ ( astronomical refraction ),  dan dapat dihitung dengan menggunakan  Hukum Snellius ( Snell’s Law ).

Kekeliruan cara pembuktian teori relativitas umum sesuai yang diminta oleh pencetus teori, Albert Einstein,  dianalisa dan dijelaskan dalam buku ' Einstein, Arthur Eddington, dan Astronomi ' yang baru dipublikasikan berupa Kindle eBook ( Amazon ),  Kobo eBook,  dan di Payloadz Store.

Einstein, Arthur Eddington, dan Astronomi - Payloadz Store

Dalam post di bawah ini disampaikan beberapa kutipan artikel untuk lebih memahami tentang  ' astronomical refraction ' atau ' lengkungan sinar astronomis '.

The apparent position of an object in the sky may be changed by several different physical effects.
One of these is refraction.

The speed of light changes as it passes through a medium such as air.

We define the refractive index of any transparent medium as 1/v,

where v is the speed of light in that medium.
The speed of light in air depends on its temperature and its pressure,
so the refractive index of the air varies in different parts of the atmosphere.
Make a simple model of the atmosphere as n layers of uniform air above a flat Earth,
with a different velocity of light vi for each layer (i from 1 to n).
Apply Snell's Law of Refraction at each boundary. 

At the first boundary, sin(i₁) / sin(r₁) = v₀ / v₁ .

At the next boundary, sin(i₂) / sin(r₂) = v₁ / v₂ , and so on.
But, by simple geometry, r₁ = i₂, r₂ = i₃ and so on.
So we have

sin(i₁) = (v₀ / v₁) sin(r₁)
          = (v₀ / v₁) sin(i₂)
          = (v₀ / v₁) (v₁ / v₂) sin(r₂)
          = (v₀ / v₂) sin(r₂)
          = ..........
          = (v₀ / v_n) sin(r_n)
In other words, the refractive indices of the intervening layers all cancel out.
The only thing that matters is the ratio between v₀
(which is c, the speed of light in vacuum)
and v_n (the speed in the air at ground level).
Now r_n is the apparent zenith distance of the star, z',
and i₁ is its true zenith distance, z.
So sin(z) = (v₀ / v_n) sin(z').
Refraction has no effect if a star is at the zenith (z=0).
But at any other position, the star is apparently raised; the effect is greatest at the horizon.
Define the angle of refraction R by R = z - z'.
Rearrange this as z = R + z'.
Then sin(z) = sin(R) cos(z') + cos(R) sin(z').
We assume R will be small, so, approximately,
sin(R) = R (in radians), and cos(R) = 0.
Thus, approximately,
     sin(z) = sin(z') + R cos(z').
Divide throughout by sin(z') to get
     sin(z)/sin(z') = 1 + R/tan(z')
which is to say,
     v₀/v_n = 1 + R/tan(z').
So we can write
     R = (v₀/v_n - 1) tan(z')
We write this as
     R = k tan(z')
where k = (v₀/v_n - 1)
Here v₀ is c, the velocity of light in a vacuum, which is constant.
But v_n depends on the temperature and pressure of the air at ground level.
At "standard" temperature (0°C = 273K) and pressure (1000 millibars),
     k = 59.6 arc-seconds.
The formula in the Astronomical Almanac is
     k = 16.27" P/(273+T)
where P is in millibars, and T is in °C.

(  www.st-and.ac.uk )




Atmospheric extinction is the reason that the best spot in the sky to observe astronomical objects is the zenith which is directly overhead. Star light travels through less atmosphere at the zenith than in any other direction. Extinction is worst at or near the horizon.

For example, you can look directly at a Sun set because the Sun's light has maximum atmospheric absorption at the horizon. When the Sun is high in the sky it is painful and dangerous to look at the Sun without optical protection.

Refraction does make a star appear higher in the sky
than it actually is.

Refraction
As stellar light passes through the atmosphere, it is refracted (bent) just as through a lens. This bending results from the increase in the atmosphere’s density as the light ray travels downward toward the observer. Thus refraction makes an object appear higher in the sky than it actually is.

( www.ngawhetu.com ) 

( www.solarplots.info )

Light is all around us, from both natural and artificial sources, during the day and the night. We think we understand it, and that what we see by it is an exact representation of what we are looking at. However we can be mistaken; the setting sun seen on the horizon has in fact already dropped below the horizon. Twinkling stars are also an effect of this same process, called refraction.

Light passing through a medium such as air or water can be absorbed and scattered by the molecules in the medium or refracted by changes in air density. Earth's atmosphere contains air, water and dust molecules that cause light rays from the sun to change direction as they pass through slightly different densities of air - this is known as refraction. 

The amount of refraction of light is dependent on the refractive index (a measure of how much a substance bends light, dependent on its density and the type of molecules) and the incident angle at which the light enters the substance. Denser substances such as water will bend the light more than a less dense substance like air, and light entering a substance at an angle will refract more than entering perpendicular to the substance's surface. Air itself can have different indices- air that is warm will be less dense and so will refract light less.

Looking up in the direction of the zenith, an observer will look through one air mass- ie the minimum amount of air that light from the sun will travel through to the surface.
Light at an angle z from the zenith will pass through more air, so travels through an equivalently greater air mass at a greater incidence angle z. Roughly, the air mass varies with secant z,
as cos(z)=1 airmass / n airmasses in a first-order case,
although for large angles (for more than about 60 degrees) away from the zenith, this is less accurate due to the spherical nature of the atmosphere.

At the horizon, light will travel through a maximum of about 38 air masses to reach an observer at sea level.

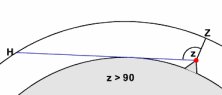
However if the observer is above sea level, for example on a mountain or in a plane, the air mass can be greater than 38, due to the line-of-sight passing through more air before reaching the observer's horizon.
This change in air mass depending on where an observer looks in the sky changes the amount and type of light reaching the observer's position. Rayleigh (1871) found that the probability of a single photon (or packet of light energy) being scattered by an air molecule was inversely proportional to its wavelength to the fourth power.

Blue light with a wavelength of about 450nm has more chance of being scattered than red light at 660nm. Light (especially the blue end of the spectrum) travelling through a greater air mass will be scattered more as there is more chance of encountering particles over this larger volume in the line-of-sight. The consequences of this are that the sun (as a single source) appears dimmer and redder near the horizon than from the zenith, as more light, especially bluer light, is scattered out of the line-of-sight to the observer.

At zenith the sun's light is not scattered as much and so only a little blue light is lost- the sun appears white or slightly yellow. Conversely skylight (light from the sun scattered onto air and water molecules and so arriving at the observer from a direction other than the sun) looks bluer as it is mostly the blue light that is scattered in all directions that reaches the observer.

Viewing Astronomical Objects

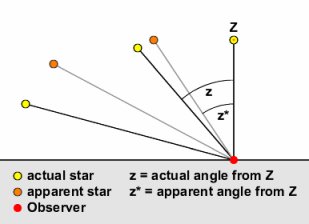
The light from stars and other objects such as the sun, moon and planets is also subject to these refractive properties which can cause the objects to appear higher in the sky than they actually are. Again, light from stars near the horizon passes through a larger volume of air at a larger incidence angle than near the zenith, therefore encountering more changes in air density and so refracts more. The observer's eyes see the star where the light appears to be coming from, not the origin of the convoluted path that it actually takes. The closer to the horizon the star is, the greater amount of refraction we see and the greater disparity in apparent position.


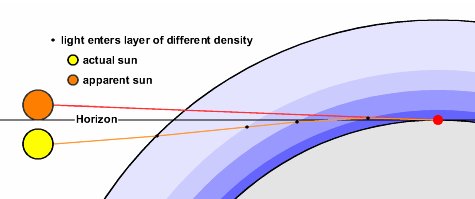
Consequently the sun or any celestial object setting on the horizon will be refracted the largest amount. As mentioned before, the angle of refraction is great enough that an observer can see the sun when it is actually below the horizon. The disk of the sun has an angular distance of about 30 arcminutes (or half a degree).

The index of refraction for dry air at sea level is about 1.0002941, which means that the amount of refraction in dry air is also quite small - about 39 arcmins, but enough that as the bottom of the sun's disk is seen to touch the horizon, the top is actually 9 arcmins below the horizon.

Twinkling Stars

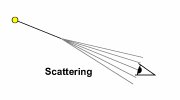Refraction also occurs with small variations in air density due to uneven heating of the air (characterized by increased winds). This leads to small amounts of refraction of a star's light that an observer sees as twinkling (also known as scintillation). Again as the star's light travels through greater air mass near the horizon, the greatest twinkling is seen at the horizon.

Two processes occur when looking at a star: light is momentarily refracted so as to appear to come from a slightly different position, and light is scattered in different directions, so decreasing the amount of light from the star that reaches the observer. These processes cause the star to appear to deviate slightly from its position, and to fade for split seconds of time, causing the star to twinkle.

Stars very near the horizon can also be seen to change colour momentarily. This is due to the light of different wavelengths (or colours) being dispersed different amounts by slight changes in the air. The star can appear any colour of the spectrum as the observer either sees the bluer light that is refracted or the redder light that is left or any colour in between before changing quickly again.

Objects with a measurable angular size such as the moon and planets do not appear to twinkle- this is due to the fact that light from the object is reaching the observer from all points on the object's disk. If one light ray is refracted out of line-of-sight, it does not make a noticeable difference to the observer, and light from the whole disk can not be deflected at the same time. There is also a chance that light from another point on the disk would be refracted into the line-of-sight so the intensity of light would not change.

An observer, therefore, can only be sure that what he is looking at is a true representation of an object if he is looking straight up to the zenith. Any view towards the horizon will be subject to increasing refractive and scattering effects, that can cause disparity in an object's position, changes in the colour of the incoming light and minute changes in the quality of light causing twinkling.

( www.math.ubc.ca )



Snell's Law

Snell's law states that the ratio of the sines of the angles of incidence and refraction is equivalent to the ratio of phase velocities in the two media, or equivalent to the reciprocal of the ratio of the indices of refraction:

with each 0 as the angle measured from the normal of the boundary, v as the velocity of light in the respective medium (SI units are meters per second, or m/s) and n as the refractive index (which is unitless) of the respective medium. ( Snell's Law  ).

If Einstein's theory of relativity was correct, then the light from stars that passed closest to the sun would show the greatest degree of "bending."  ( undsci.berkeley.edu )

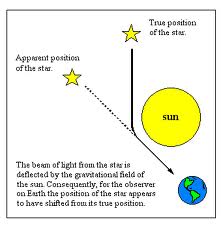
Sesuai gambar di atas,  jika teori relativitas umum benar,  maka :

1. Cahaya dari bintang-bintang yang berlalu dekat dengan medan gravitasi matahari akan menunjukkan tingkat terbesar pembelokannya.

2.  Semakin jauh dari medan gravitasi matahari,  sudut penyimpangannya akan semakin kecil.

3. Dan ketika cahaya bintang-bintang itu bebas dari medan gravitasi matahari,  maka tidak ada perbedaan antara posisi sejati dan posisi semu bintang.

Dari gambar dan penjelasan di atas dapat diartikan,  ketika malam hari cahaya bintang-bintang bebas dari medan gravitasi matahari,  maka tidak ada perbedaan antara posisi sejati dan posisi semu bintang. 

Hal tersebut di atas adalah sesuatu yang tidak mungkin.  Gambar di atas  bisa menjelaskan bahwa hipotesis cahaya membelok di medan gravitasi benda masif,  adalah tidak benar alias keliru.  Benda-benda angkasa atau  bintang-bintang yang dilihat oleh para mengamat,  baik dengan menggunakan alat maupun melihatnya dengan mata telanjang, semuanya menunjukkan posisi semu ( observed / apparent position ) dan bukan posisi sejatinya ( actual / true position ). Dan memang ada ' pembelokan cahaya ', tetapi bukan disebabkan karena gravitasi,  melainkan karena adanya refraksi sinar ( astronomical refraction ).  Sudut pembelokan bisa dihitung dengan menggunakan Hukum Snellius ( Snell's Law ).

Catatan :  Gambar ilustrasi dari undsci.berkeley.edu di atas bisa digunakan untuk menjelaskan kekeliruan hipotesis Enstein,  namun gambar ilustrasi itu sendiri sebenarnya kurang cermat.  Observed / apparent position of star selalu tampak oleh penilik di bumi lebih tinggi dari  true / actual position.  

The effect of astronomical refraction is to make a celestial body appear higher in the sky than it otherwise would.

Sehingga penggambaran di slide yang digunakan untuk pengajaran astronomi, apparent position harus  diletakkan di atas actual position.  Sehingga urut-urutan gambar di atas seharusnya matahari digambar agak ke bawah, lalu diatasnya gambar no.1, no.2,dan no.3 masing-masing dengan posisi apparent position di atas actual position.